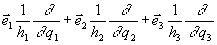
The derivation, which closely follows Margenau
and Murphy, is done in a generalised coordinate system and later
transformed to spherical polar.
The Generalised System:
| Coordinates | |
| Infinitismal displacements | |
| Volume element | |
| Displacement vector | |
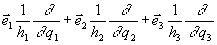 |
![]()
In the Spherical
Polar System, we have,
q1 = r q2 = qq3
= f
dV = r2sinqdq df
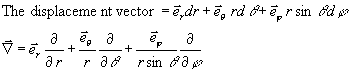
Working in the generalised system,
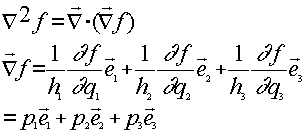
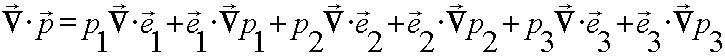 Eqn
(2)
Eqn
(2)
Let us evaluate the first two terms (the others will follow
similarly)
The second term is equal to 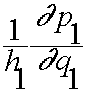
The first term needs more work:

--Verify the above result by writing the triple products
in determinantal form.
We will now evaluate 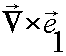
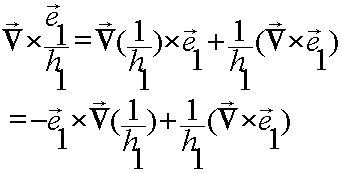
(Note that ![]() )
)
Therefore,
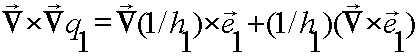 The L.H.S.
is a curl of a gradient, and therefore, equal to zero, which leads to,
The L.H.S.
is a curl of a gradient, and therefore, equal to zero, which leads to,
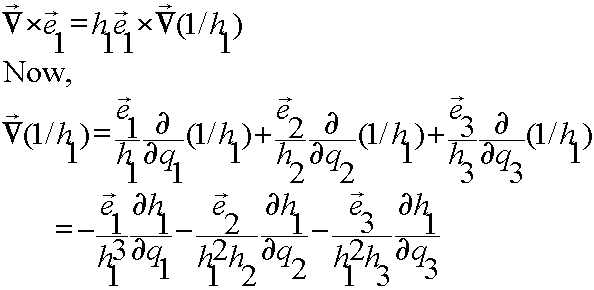
![]()
![]()
![]() Giving,
Giving,
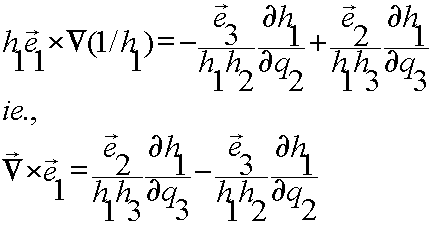
![]() In the above
equation, one can cyclically permute the subscripts. Substituting the results
in Eqn (3) gives,
In the above
equation, one can cyclically permute the subscripts. Substituting the results
in Eqn (3) gives,
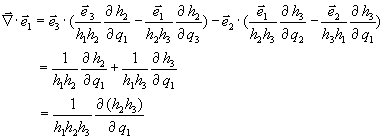
![]()
![]() Substituting
in Eqn (2),
Substituting
in Eqn (2),
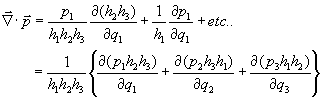
![]()
Combining the above result with Eqn (1),
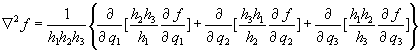
Reverting to the spherical polar coordinate system, we
have,
h1 = 1, h2 = r, h3 = rsinq, so that,
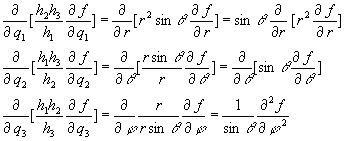
and finally,
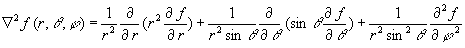
(Check carefully and find some errors !)