The Variation Principle

If f is a well behaved function satisfying the boundary conditions, then, the ground state energy E₁ satisfies the inequality,

f may be expressed in terms of certain parameters which are varied so as to minimize the LHS of the above inequality. In general, f approaches the true wave function much more slowly than the variation integral approaches E₁.

It is often convenient to express f as a linear combination and to vary the coefficients in the expansion to minimize the variational integral.

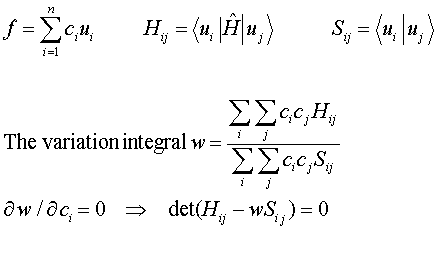
The solution of the above secular equation gives n possible values for the energies (w₁….w_n). It turns out that if, the true energies of the various states are ordered as E₁ < E₂ <..< E_n , and if w₁ < w₂ <….< w_n, then,

The secular equation may be simplified by choosing the u’s in such a way that they form an orthonormal set (this makes the off-diagonal S_ij zero) and by choosing them to be eigenfunctions of some operator(s) which commute(s) with the Hamiltonian (this makes some of the off-diagonal H_ij to vanish)