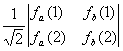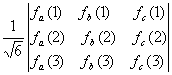Permutation operator and the Pauli principle
The
permutation operator interchanges the coordinates of any two particles in a
wave function involving the coordinates of n identical particles.
![]()
![]()
(Operators,
such as above, whose square is a unit operator have eigenvalues, +1 or –1.)
In
the above equation the + sign applies to bosons and the – sign to fermions. The
electronic wave functions are therefore, antisymmetric in the exchange of any
two electrons. This is known as the Pauli principle.
Due
to the properties of determinants, wave functions written as determinants
satisfy the Pauli principle. Such wave functions are referred to as Slater
determinants.
Tw
examples:
|
|
2e-function |
3e-function |
|
Simple
product function |
|
|
|
Antisymmetric
linear combination |
|
|
|
Determinantal
form |
|
|
|
Slater
determinant in short hand notation |
|
|
In
general, the single determinantal form of an n-electron wave function is
written as

Often,
the ui’s are spin-orbitals, ie., they are products of a space
(or orbital) part and a spin part. For example, one may have,
![]()