Secular equation

when S_ij = d_ij (ie., when the secular determinant is constructed on an orthonormal basis),

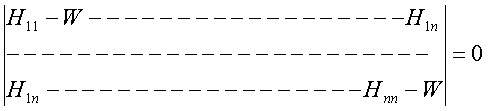
This equation can be solved by diagonalising the corresponding (Hermitian) matrix. This can be done numerically by performing an unitary transformation (or orthogonal transformation if the matrix is real symmetric). See CH413 notes.