Special Functions

 

An important type of ordinary differential equations is,

 

y'' + P(x) y' + Q(x) y = 0

 

 
 

P(x)

Q(x)

Hermite equation

Legendre equation

Associated Legendre equation

Laguerre equation

Associated Laguerre equation

Under certain conditions, the above equations have polynomial solutions.

 

Hermite polynomials : a = n, an integer >/= 0

 

n

Hn(x)

0

1

1

2x

2

4x2 - 2

3

8x3- 12x

Hn+1(x) = 2xHn(x) - 2nHn-1(x)

If the Hermite equation is modified with P(x) = 0, and Q(x) = 1 - x2 + 2n, there results the Hermite-Gauss equation. Its solutions are . When normalised by multiplying with these become the wave functions of the harmonic oscillator.

 

Legendre polynomials : x in the range -1 to 1 and l, an integer > = 0

 

 

l

Pl(x)

0

1

1

x

2

(1/2)(3x2 -1)

3

(1/2)(5x3-3x)

 

Pl+1(x) = [x(2l + 1)Pl(x) - lPl-1(x)] / (l + 1)

 

 

Associated Legendre polynomials : integer m < = l

 

l

m

0

0

1

1

0

x

1

1

(1 - x2)1/2

2

0

(1/2)(3x2 - 1)

2

1

3x(1 - x2)1/2

2

2

3(1 - x2)

 

 

 

Spherical harmonics :

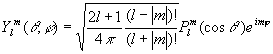
These are the wave functions of the rigid rotor. They also serve as the angular part of the hydrogen atom wave functions.

 

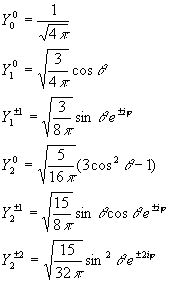
Laguerre polynomials : a = n, an integer > =1

 

1 - x

x2 - 4x + 2

-x3 + 9x2 - 18x + 6

x4 - 16x3 + 72x2 - 96x + 24

-x5 + 25x4 - 200x3 + 600x2 - 600x + 120

Associated Laguerre polynomials : integer k > = 0

The radial part of the hydrogen atom wave functions are obtained as,

, where n is the principal quantum number and r is proportional to the radial coordinate of the electron ( r = 2r/nao).

 

------------------------------------------

 

References : Eyring, Walter and Kimball "Quantum Chemistry"

Margenau and Murphy "Mathematics of Physics and Chemistry"